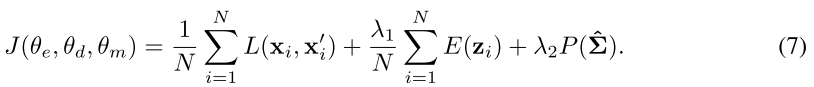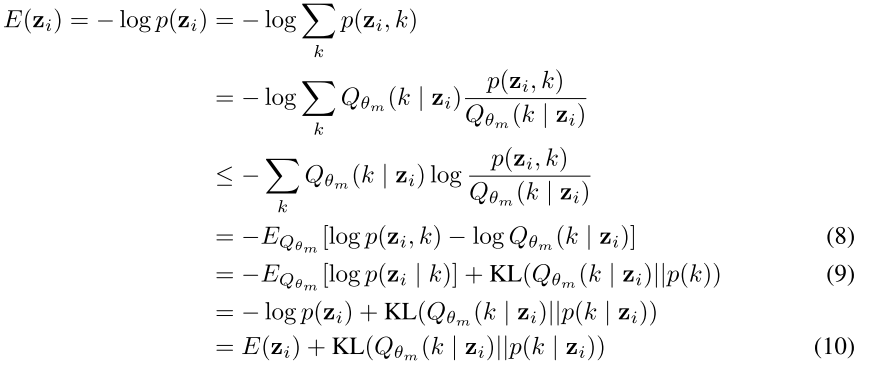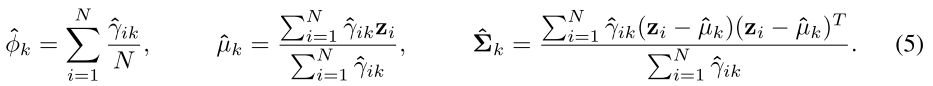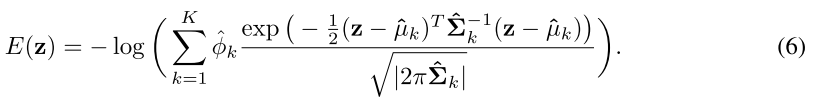Deep Autoencoding Gaussian Mixture Model for Unsupervised Anomaly Detection
Deep Autoencoding Gaussian Mixture Model for Unsupervised Anomaly Detection
https://openreview.net/forum?id=BJJLHbb0-
1. どんなもの?
画像を深層オートエンコーダを使用して次元削減したものをガウス混合モデルで密度推定して異常検知を行う
2. 先行研究と比べてどこがすごい？
深層オートエンコーダの学習による次元削減とEMアルゴリズムによるガウス混合モデルを別々で学習していた
別々で学習すると、異常検知で重要なデータが次元削減の段階で取り除かれてしまう可能性がある
そこで、次元削減と密度推定を同時に学習
3. 技術や手法の”キモ”はどこ？
変数定義
目的関数
$L()$: 再構成誤差を求める損失関数(L2ノルムなど)
$E(z_i)$: 入力サンプルの観測確率のモデル化
$P()$: 特異点問題(共分散行列の対角線上のエントリが０に縮退すると、矮小な解が誘発される問題)を回避するためのペナルティ
$\lambda_1,\lambda_2$: メタ・パラメータ
$Q_{\theta m}$: メンバーシップ予測の推定ネットワーク
$p(z_i,k)$: $z_i$が与えられた混合成分kの事後確率分布
COMPRESSION NETWORK
$x$: 入力画像
$z_c$: AEの潜在変数
$x’$: 再構成画像
$z_r$: 絶対ユークリッド距離、相対ユークリッド距離、コサイン類似度などの複数の距離指標を考慮した多次元
$f()$: 再構成誤差を計算する関数
$z$: COMPRESSION NETWORKが抽出した低次元特徴
ESTIMATION NETWORK
$MLN()$: 推論に使用するネットワーク
$\hat{\gamma}$: メンバーシップ予測のためのK次元ベクトル
$\hat{\phi}_k$: GMMにおける成分kの混合確率
$\hat{\mu}_k$: GMMにおける成分kの平均
$\hat{\Sigma}_k$: GMMにおける成分kの共分散
$E(z)$: 異常予測に使用するサンプルエネルギー
学習
目的関数
N個のサンプルのデータセットにおける目的関数
再構成誤差$L$と下述$E$とペナルティ$P$
$E$は$z_i$が与えられた混合成分kの事後確率分布$p(z_i,k)$と
メンバーシップ予測の推定ネットワーク$Q_{\theta m}$の分布を(8)を最小化することで近づける
推論（異常度の算出）
COMPRESSION NETWORK
エンコーダから潜在変数$z_c$を取得
入力画像とデコーダの再構成画像の誤差を計算
$ x’ = Decoder(z_c) $
$ z_r = f(x,x’) $
抽出した$z_c$と$z_r$を組み合わせて$z$を作成
ESTIMATION NETWORK
推定ネットワークを利用してメンバーシップ予測のためのK次元ベクトル$\hat{\gamma}$を予測
$ \hat{\gamma} = softmax(MLN(z)) $
それを用いてGMMのパラメータ、混合確率$\hat{\phi}_k$・平均$\hat{\mu}_k$・共分散$\hat{\Sigma}_k$を推定
上のパラメータを用いて、サンプルエネルギー(確率密度のエントロピー？)を推定
4. どうやって有効だと検証した？
KDDCUP, Thyroid, Arrhythmia, KDDCUP-Revで実験
異常検知のF1スコアが最大で14％向上
6. 関連文献
Shuangfei Zhai, Yu Cheng, Weining Lu, and Zhongfei Zhang. Deep structured energy based models for anomaly detection. In International Conference on Machine Learning, pp. 1100–1109, 2016.
