軸屋敬介 | Keisuke Jikuya

Home Blog Note Post

q-Space Novelty Detection with Variational Autoencoders

https://arxiv.org/abs/1806.02997

Jul 29, 2021

Anomaly Detection, Unsupervised Learning, VAE,

CDMRI (2020)

1. どんなもの?

• 正常なデータを用いた変分オートエンコーダー（VAE）の学習に基づく多発性硬化症（MS）患者のdMRIスキャンにおける新規性検出法

2. 先行研究と比べてどこがすごい？

変分オートエンコーダー（VAE）に基づいて、
確率的，距離ベース，再構成ベースの新規性検出法をいくつか設計した。

3. 技術や手法の”キモ”はどこ？

変数定義

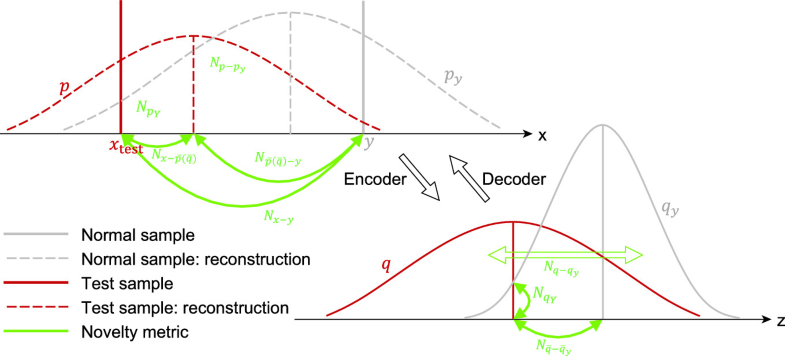
• $x_{test}$: テストサンプル
• $E()$: エンコーダ出力
• $N_(x_{test})$: 新規性スコア

学習

• 正常データを捉えるように学習
• 損失関数は通常と同じ
  • \[L_{VAE} = -\sum_i ELBO_i = -\sum_i \big[E_{q_\phi(z|x_i)}\big[log p_\theta(x_i|z)\big] - D_{KL}(q_\phi(z|x_i)||p(z))\big]\]

推論（異常度の算出）

• 潜在空間における新規性
  • VAE正規化スコア
    • \[N_\text {VAE-reg}({x_\mathrm {test}}) = {D_\mathrm {KL}}\big (q_\phi (z|{x_\mathrm {test}}) \parallel \mathcal {N} (0,I)\big )\]
    • 異常なサンプルは、正常なサンプルよりも単位ガウスからより多く発散する潜在空間内の分布を持つことが予想される
    • そこで、新規性スコアはVAE損失関数のKLダイバージェンス項を使用
  • 潜在空間距離
    1. 分布の平均間のユークリッド距離
       テストデータポイントの潜在空間分布の平均と，正常なサンプルの最も近い潜在空間分布の平均との間の距離
       • \[N_{\bar{q}-\bar{q}_y}({x_ \mathrm {test}}) = \min _{y \in Y}\left\| E[q_ \phi (z|{x_ \mathrm {test}})] - E[q _\phi (z|y)]\right\| _2^2\]
    2. 分布間のBhattacharyaa距離
       Bhattacharyya距離 : 2つの確率分布pとqの非類似性を表す対称的な尺度\(D_B(p,q) = -{\ln \big(\mathrm {\int \sqrt{p(z)q(z)} {\,\mathrm {d}}z}(p,q)\big )}\) 新規性スコアはテストサンプルの潜在空間分布$q_\phi (z|{x_\mathrm {test}})$と正常サンプルの最も類似した潜在空間分布$q_\phi (z|y)$との間の距離
       • \[N_{q-q_y}({x_\mathrm {test}}) = \min_{y \in Y}D_B(q_\phi (z|{x_\mathrm {test}}), q_\phi (z|y))\]
  • 潜在空間における密度ベースの距離
    潜在空間における正常なデータの密度を推定\(q_Y(z)=\frac{1}{|Y|}\sum_{y \in Y} q_\phi (z|y)\) それを利用して新規性スコアを計算
    • \[N_{q_Y}({x_\mathrm {test}}) = -q_Y(E[q_\phi (z|{x_\mathrm {test}})])\]
• オリジナルの機能空間における新規性
  • VAE再構築ベース
    VAEはエンコーダ、デコーダともに確率的なので、サンプルを抽出したり平均をとって対応
    3.~6.のmeanに関してはmin計算に置き換え可
    1. 決定論的再構成エラー
       入力を決定論的に再構成し、再構成誤差を計算
       • \[N_{x-\bar{p}(\bar{q})}({x_\mathrm {test}}) = \left\| {x_\mathrm {test}}- E\big [p_\theta \big (x|E[q(z|{x_\mathrm {test}})]\big )\big ]\right\| _2^2\]
    2. 決定論的再構築の可能性
       エンコーダの平均値を与えられた入力の対数尤度を計算
       • \[N_{\bar{p}(\bar{q})}({x_\mathrm {test}}) = - \log p_\theta \big({x_\mathrm {test}}| E\big[q(z|{x_\mathrm {test}}\big )\big]\big)\]
    3. エンコーダー確率的再構成エラー
       エンコーダのサンプルとデコーダの平均値を使って、入力の可能な再構成をいくつか計算し、平均再構成誤差を算出
       • \[N_{x-\bar{p}(\hat{q})}({x_\mathrm {test}}) = \underset{z_i \sim q_\phi(z|x_{test})}{mean} \left\| {x_\mathrm {test}}- E\big [p_\theta \big (x|z_i)]\right\| _2^2\]
    4. エンコーダー確率的再構成の可能性
       エンコーダからのサンプルが与えられたときに、入力の対数尤度関数値をいくつか計算
       • \[N_{\bar{p}(\hat{q})}({x_\mathrm {test}}) = \underset{z_i \sim q_\phi(z|x_{test})}{mean} - \log p_\theta (x_{test}|z_i)\]
    5. デコーダー-確率的再構成エラー
       エンコーダの平均値とデコーダからのサンプルを使って、平均再構築誤差を計算
       • \[N_{x-\hat{p}(\bar{q})}({x_\mathrm {test}}) = \underset{x_i \sim p_\theta \big (x\big |E\big [q_\phi(z|x_{test})\big ]\big )}{mean} \left\| {x_\mathrm {test}}- x_i\right\| _2^2\]
    6. 完全確率的再構成エラー
       エンコーダとデコーダの両方のサンプルを使用して、平均再構成誤差を計算
       • \[N_{x-\hat{p}(\hat{q})}({x_\mathrm {test}}) = \underset{z_i \sim q_\phi(z|x_{test})}{\underset{x_i \sim p_\phi(x|z_i)}{mean}} \left\| {x_\mathrm {test}}- x_i\right\| _2^2\]
  • 距離ベースおよび密度ベース
    1. 前述の再構成に
       • ユークリッド距離を適用
         • \[N_{\bar{q}-\bar{q}_y}({x_\mathrm {test}}) = \min _{y \in Y}\left\| E[p_\theta(x|E[q_\phi (z|{x_\mathrm {test}})])] - E[p_\theta(x|E[q_\phi (z|y)])]\right\| _2^2\]
       • Bhattacharyaa距離を適用
         • \[N_{q-q_y}({x_\mathrm {test}}) = \min_{y \in Y}D_B\big(p_\theta(x|E[q_\phi (z|{x_\mathrm {test}})]), p_\theta(x|E[q_\phi (z|y)]\big)\big)\]
       • 密度を適用
         • \[N_{q_Y}({x_\mathrm {test}}) = -p_Y\big(E\big[p_\theta\big(x|E[q_\phi (z|{x_\mathrm {test}})])\big]\big)\]
    2. 1.の
       • 上の式に決定論的再構成の代わりに元のテストサンプルを使用
         • \[N_{x-\bar{p}(\bar{q}_y)}({x_\mathrm {test}}) = \min_{y \in Y} \left\| x_{test} - E\big [p_\theta \big ( x\big|E\big[q_\phi(z|y)\big] \big) \big] \right\| _2^2\]
       • 下の式にに決定論的再構成の代わりに元のテストサンプルを使用
         • \[N_{p(\bar{q}_Y)(x)}({x_\mathrm {test}}) = -p_Y(x_{test})\]
    3. 再構成とオリジナルでユークリッド距離
       • \[N_{\bar{p}(\bar{q})-y}({x_\mathrm {test}}) = \min_{y \in Y} \Bigl \Vert E\big [p_\theta \big (x|E[q_\phi (z|{x_\mathrm {test}}) - y]\big )\big ]\Bigr \Vert _2^2\]
  • 最も近い生成されたサンプルまでの距離
    入力とVAEデコーダが生成できる最も近いサンプルとの距離
    • \[N_{x-\hat{p}}({x_\mathrm {test}})=\min _{z}\left\| {x_\mathrm {test}}- E[p_\theta (x|z)]\right\| _2^2\]
  • 生成された最高の可能性の反数
    ユークリッド不使用で、$p_{\theta} (x_{test}|z)$の密度値を計算
    • \[N_{\hat{p}}(x_{test}) = \min_z - \log p_{\theta} (x_{test}|z)\]
• VAE損失としての新規性
  • VAEの損失関数$L_{VAE}$そのものが新規性の指標
    • \[N_{-\mathrm {ELBO}}({x_\mathrm {test}}) = -E_{q_\phi (z|{x_\mathrm {test}})}[\log p_\theta ({x_\mathrm {test}}|z)] + {D_\mathrm {KL}}\big (q_\phi (z|{x_\mathrm {test}})\parallel \mathcal {N}(0,I)\big )\]
  • 確率的複合器 \(q_{\phi}\) \((z\|{x_{\mathrm{test}}})\) からの複数サンプルを使用
    • \[N_{-{\widehat{\mathrm {ELBO}}}}({x_{\mathrm {test}}}) = \min_{z\sim q_{\phi} (z|{x_{\mathrm{test}}})}[\log p_{\theta} ({x_{\mathrm{test}}}|z)] + {D_{\mathrm{KL}}}\big (q_{\phi} (z|{x_{\mathrm {test}}})\parallel \mathcal{N}(0,I)\big )\]

4. どうやって有効だと検証した？

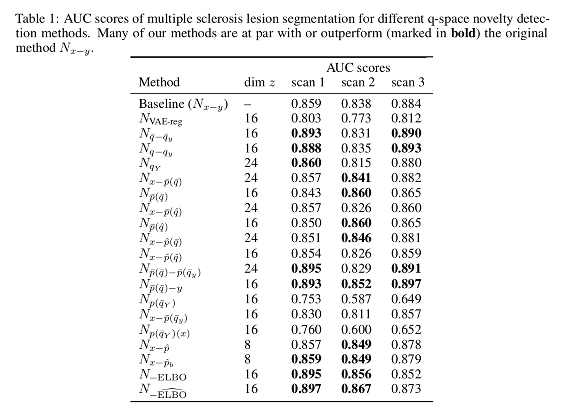
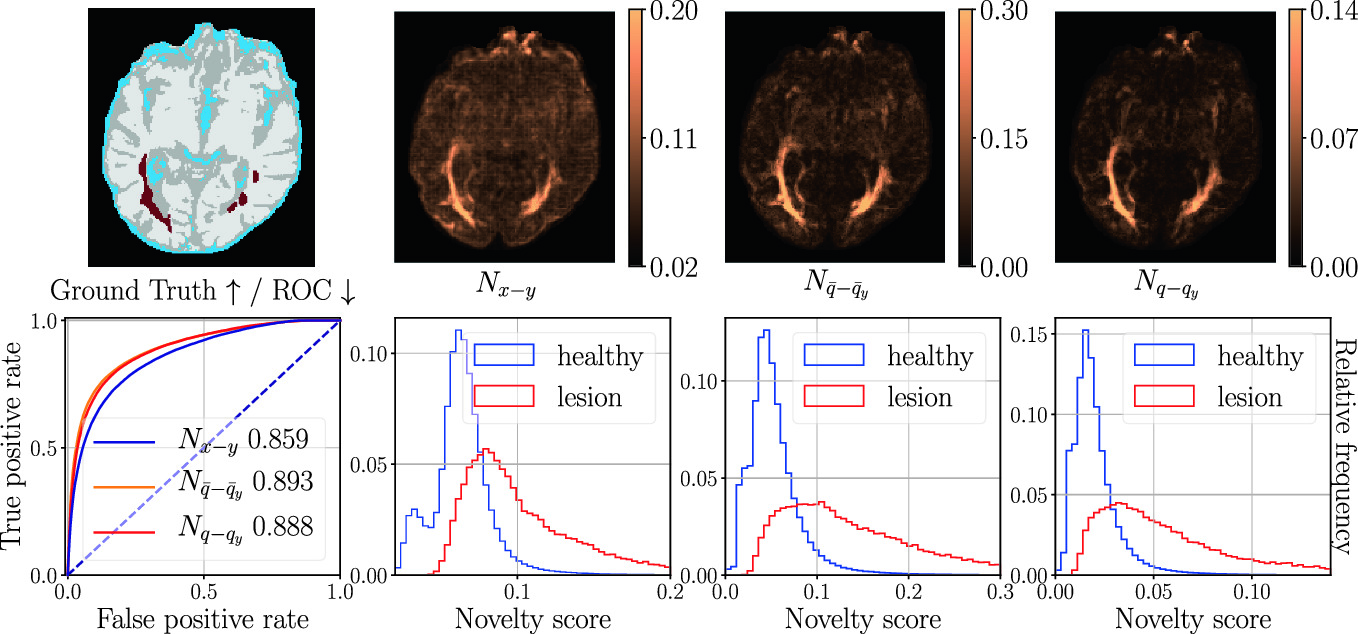
• 多発性硬化症患者の拡散MRIスキャンにおける拡散空間（q-space）異常の検出(多発性硬化症の病変を検出)
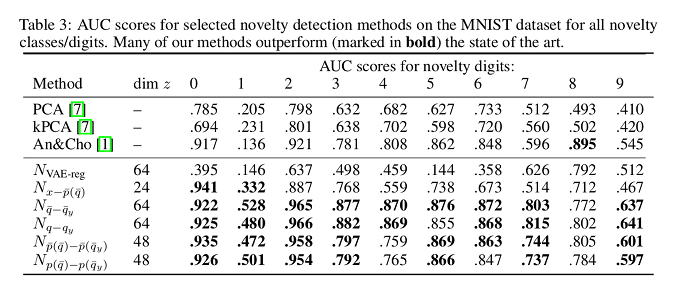
• MNIST
  

6. 関連文献

1. J. An and S. Cho. Variational Autoencoder based Anomaly Detection using Reconstruction Probability. Technical Report. SNU Data Mining Center, 2015.