Efficient GAN-based anomaly detection

Efficient GAN-based anomaly detection
https://arxiv.org/abs/1802.06222
Aug 17, 2021
Anomaly Detection, Unsupervised Learning, GAN,
ICDM (2018)
1. どんなもの?
- GANベースの異常検知手法
- 学習中に生成器Gと識別器Dとともに、入力サンプルxを潜在表現$z$にマッピングするエンコーダEを同時に学習
- これにより、計算量の多い潜在表現$z$の探索を回避
- 識別器は、画像だけでなく潜在表現$z$も考慮
2. 先行研究と比べてどこがすごい?
- 画像から潜在表現$z$を探すEncoderも同時に学習することで、AnoGANでネックになっていた探索の手間を省き数百倍高速に
3. 技術や手法の”キモ”はどこ?
変数定義
- $D$: 判別機
- $E$: エンコーダ
- $G$: 生成器
- $x \sim p_{X} (x)$: データの分布
- $z \sim p_{E} (z|x)$: データをエンコーダに通した分布
- $z \sim p_{Z} (z)$: 潜在変数の分布
- $x \sim p_{G} (x|z)$: 潜在変数をジェネレータに通した分布
- $A(x)$: 異常スコア関数
- $L_G$: 再構成誤差
- $L_D$: 分類機ベース誤差
学習

- BiGANの構造を用いたmin maxゲーム
-
\[\min_{E,G} \max_{D} V(D,E,G) = \mathbb{E}_{x \sim p_X} [\mathbb{E}_{z \sim p_{E}(\cdot | x)}[\log D(x,z)]] + \mathbb{E}_{z \sim p_Z} [\mathbb{E}_{x \sim p_G(\cdot | z)}[1 - \log D(x,z)]]\]
- 右辺第一項 \(\mathbb{E}_{x \sim p_{X}} [\mathbb{E}_{z \sim p_{E}(\cdot \| x)}[\log D(x,z)]]\)
- 元画像$x$とそれをエンコーダに通した潜在変数$E(x)$を識別器に入れている
- 識別器は元画像なので、これを本物1と出力するように学習
- エンコーダは本物なのに識別機に偽物0であると騙すように学習
- 右辺第二項 \(\mathbb{E}_{z \sim p_{Z}} [\mathbb{E}_{x \sim p_{G}(\cdot \| z)}[1 - \log D(x,z)]]\)
- 潜在変数$z$とそれを生成器に通した画像$G(z)$を識別機に入れている
- 識別機は生成画像なので、これを偽物0と出力するように学習
- 生成器は生成画像を識別機が本物1と騙されるように学習
推論(異常度の算出)

- 異常度$A(x)$は以下のように定義できる
-
\[A(x) = \alpha L_G(x) + (1 - \alpha ) L_D(x)\]
-
\[L_G(x) = \| x - G(E(x)) \|_1\]
- 元画像と画像をエンコーダに通して見つけた潜在変数zから生成した画像との再構成誤差
- $L_D(x)$は2種類
- 識別機がデータ分布から得られたか判断する交差エントロピー誤差
-
\[L_D(x) = \sigma \big( D \big(x,E(x)\big) , 1 \big)\]
- 識別機の中間層を比較し正常と似た特徴を持つか判断する特徴マッチング誤差
-
\[L_D(x) = \| f_D(x,E(x)) - f_D(G(E(x)),E(x)) \|_1\]
4. どうやって有効だと検証した?
- MNIST
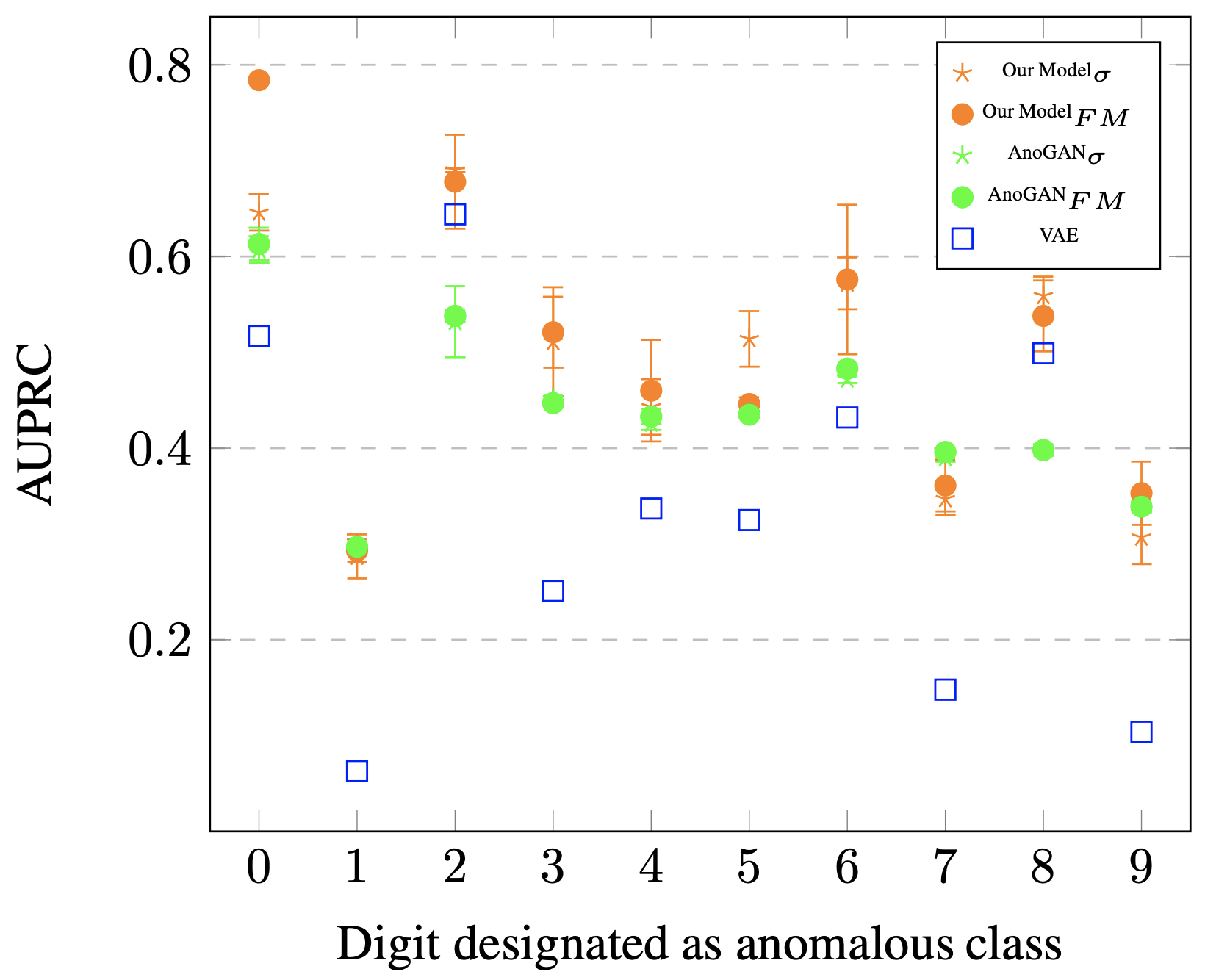
- $\sigma$ が交差エントロピー誤差
- $FM$ が特徴マッチング誤差
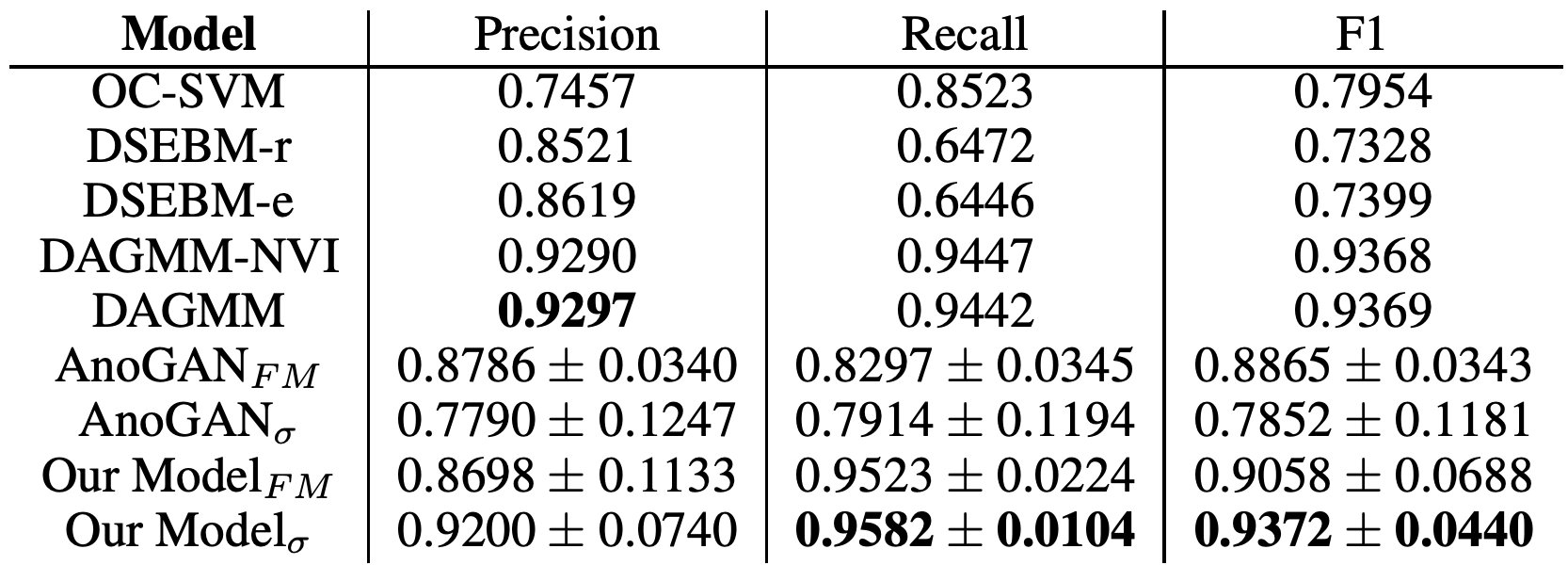
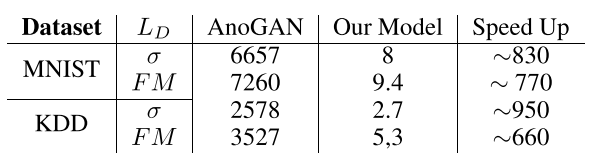
- KDDCUP99
- かかる時間のAnoGANとの比較