GANomaly: Semi-supervised Anomaly Detection via Adversarial Training
GANomaly: Semi-supervised Anomaly Detection via Adversarial Training
https://arxiv.org/abs/1805.06725
Aug 18, 2021
Anomaly Detection, Unsupervised Learning, GAN,
ACCV (2018)
1. どんなもの?
- オートエンコーダとGANを組み合わせた異常検知
- ジェネレータをオートエンコーダのような構造にし、生成画像に判別機とは別にエンコーダをつけた
2. 先行研究と比べてどこがすごい?
- あらゆる異常検出タスクに一般化できる能力を持ち,最新のGANベースの異常検出アプローチと従来のオートエンコーダベースの異常検出アプローチの両方を上回ることがわかった
3. 技術や手法の”キモ”はどこ?
変数定義
- $x$: 元画像
- $\hat{x}$: 生成画像
- $G(\cdot)$: 生成器
- $E(\cdot)$: エンコーダ
- $G_E(\cdot)$: 生成器のエンコーダ
- $f(\cdot)$: 判別機の中間層出力
- $w_{adv}, w_{con}, w_{enc} $: 調整用重み付けパラメータ
学習
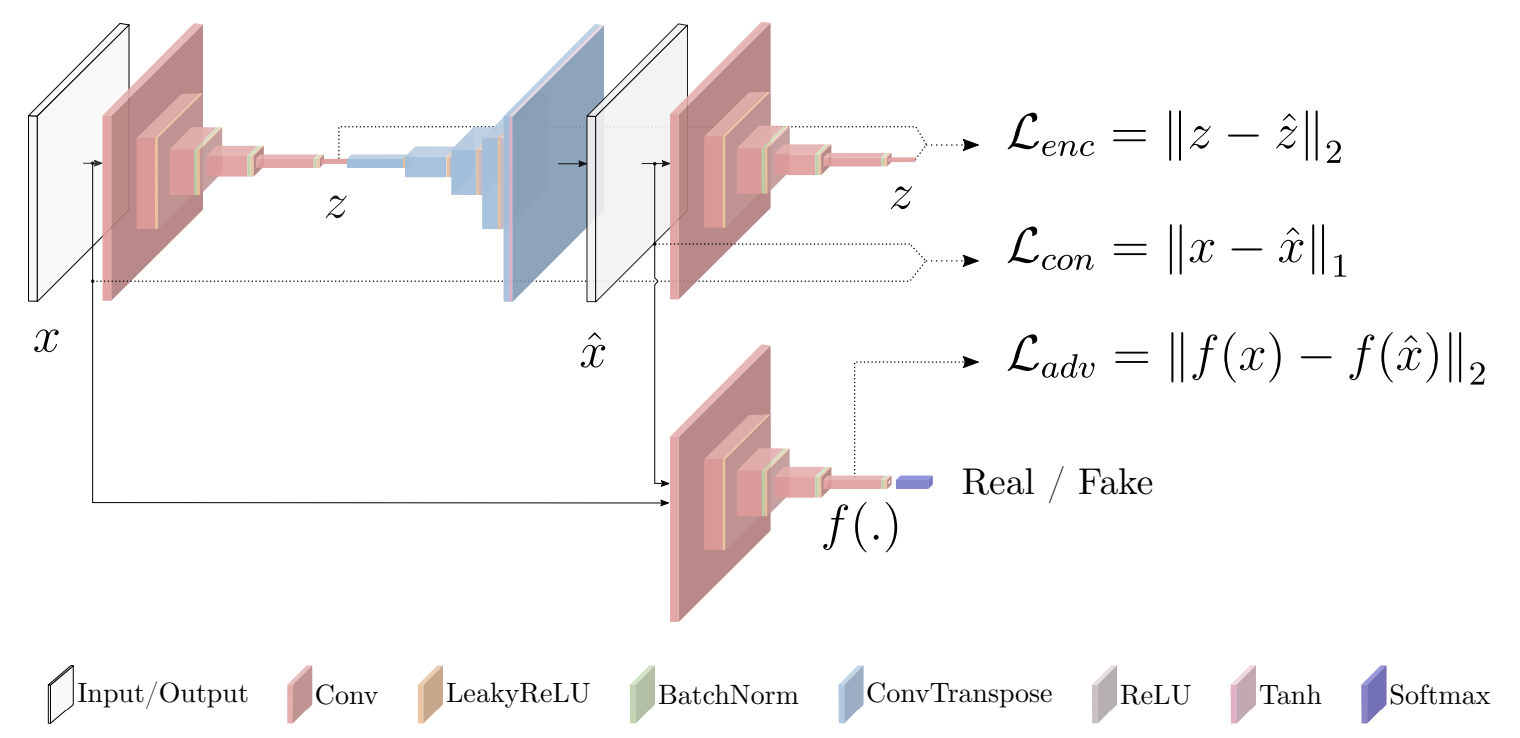
- ネットワーク構造
- 目的関数
-
\[\mathcal{L} = w_{adv} \mathcal{L}_{adv} + w_{con} \mathcal{L}_{con} + w_{enc} \mathcal{L}_{enc}\]
- Adversarial Loss
-
\[\mathcal{L}_{adv} = \mathbb{E}_{x \sim pX} \| f(x) - \mathbb{E}_{x \sim pX} f\big(G(x) \big) \|_2\]
- 元画像と生成画像を識別機に入れた中間層のL2距離
- Contextual Loss
-
\[\mathcal{L}_{con} = \mathbb{E}_{x \sim pX} \| x - G(x) \|_1\]
- 元画像と生成画像のL1距離
- Encoder Loss
-
\[\mathcal{L}_{enc} = \mathbb{E}_{x \sim pX} \| G_E(x) - E(G(x)) \|_2\]
- 元画像のボトルネック特徴と生成画像の潜在特徴のL2距離
推論(異常度の算出)
- 推論時は学習時のEncoder Lossを使用
-
\[\mathcal{A}(\hat{x}) = \| G_E ( \hat{x} ) - E (G( \hat{x})) \|\_1\]
4. どうやって有効だと検証した?
- MNISTとCIFAR10
-
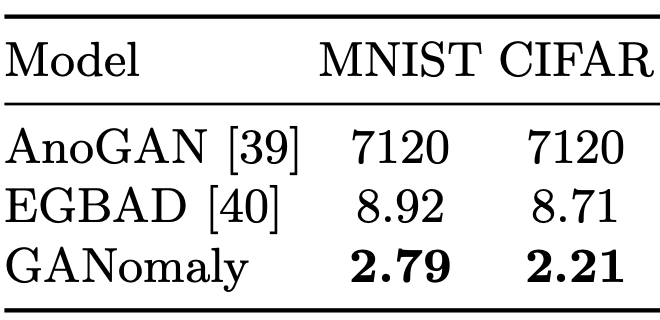
- UBAとFFOB
- X線セキュリティ検査